Mastering Geometry: How To Find Missing Side Of Triangle With Ease
Triangles are one of the most fundamental shapes in geometry, and understanding how to calculate their missing sides is a critical skill in mathematics. Whether you're solving problems for school, preparing for exams, or applying concepts in real-world scenarios, knowing how to find the missing side of a triangle can save you time and effort. This process involves leveraging mathematical principles, such as the Pythagorean theorem, trigonometry, and proportional relationships.
In this article, we'll explore everything you need to know about finding the missing side of a triangle. We’ll cover methods for right triangles, non-right triangles, and special cases like isosceles and equilateral triangles. You’ll discover how to apply formulas, use tools like sine, cosine, and tangent, and tackle both simple and complex problems with confidence. Plus, we’ll answer common questions and provide expert tips to ensure you grasp these concepts fully.
Whether you’re a student, teacher, or just a curious learner, this guide will provide you with a step-by-step approach to mastering triangle calculations. By the end of this article, you’ll not only understand how to find the missing side of a triangle but also gain practical insights into why these methods work. Let’s dive in!
- Exceptional Care And Expertise At Pine Bush Dental
- Why Dukes In Huntington Beach Is The Ultimate Coastal Dining Experience
Table of Contents
- What is a Triangle?
- Why is it Important to Find the Missing Side of a Triangle?
- Methods to Find Missing Side in Right Triangles
- How to Find Missing Side in Non-Right Triangles?
- Special Triangle Cases
- How Does Trigonometry Help in Triangle Calculations?
- What Tools Can You Use to Solve Triangle Problems?
- Practical Applications of Triangle Calculations
- Common Mistakes to Avoid
- Frequently Asked Questions
- Conclusion
What is a Triangle?
A triangle is a three-sided polygon that is characterized by its vertices (corners), edges (sides), and interior angles. The sum of a triangle's interior angles is always 180 degrees. Triangles can be classified based on their side lengths (equilateral, isosceles, or scalene) or their angles (acute, right, or obtuse).
Why is it Important to Find the Missing Side of a Triangle?
Understanding how to find the missing side of a triangle is essential for solving geometric problems in mathematics, physics, engineering, and architecture. It allows you to:
- Calculate areas and perimeters.
- Solve real-world problems involving distances and heights.
- Understand the relationships between angles and sides in different triangle types.
Methods to Find Missing Side in Right Triangles
Using the Pythagorean Theorem
The Pythagorean theorem is a fundamental principle in geometry for right triangles. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
- Finding The Perfect Jewelry Store Mejuri Near Me
- The Ultimate Guide To Adam Sandler Day Outfits Tips Trends And Style
Formula: a² + b² = c², where c is the hypotenuse.
Steps:
- Identify the sides of the triangle: the two legs and the hypotenuse.
- Plug the known values into the formula.
- Solve for the missing side by isolating the variable.
Applying Trigonometric Ratios
Trigonometric ratios such as sine, cosine, and tangent are particularly useful when one angle and one side are known, but not the hypotenuse.
Formulas:
- Sine:
sin(θ) = opposite/hypotenuse - Cosine:
cos(θ) = adjacent/hypotenuse - Tangent:
tan(θ) = opposite/adjacent
How to Find Missing Side in Non-Right Triangles?
Using the Law of Sines
The Law of Sines is helpful when two angles and one side (AAS or ASA) of a triangle are known, or when two sides and one non-included angle (SSA) are given.
Formula: (a/sin(A)) = (b/sin(B)) = (c/sin(C))
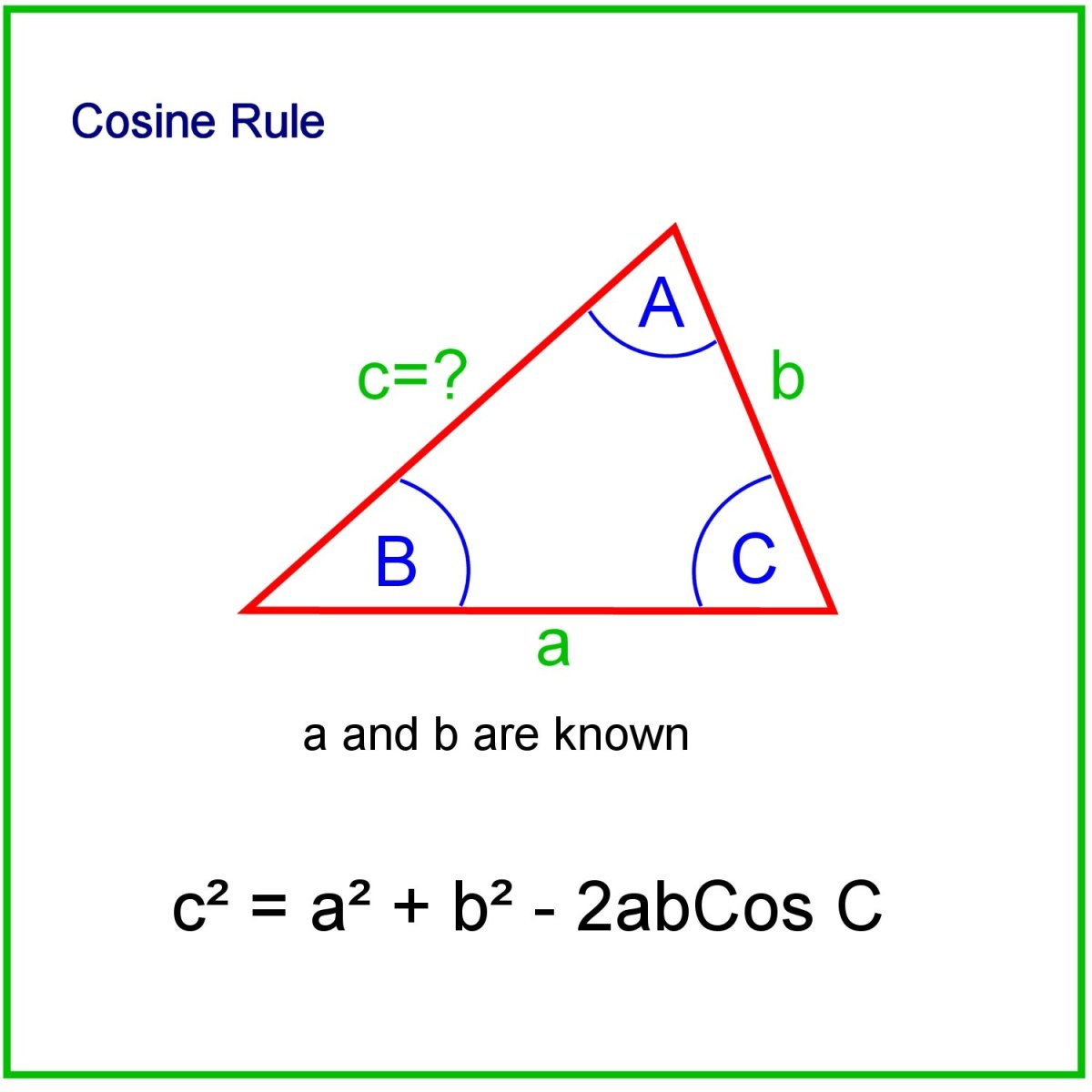
Using the Law of Cosines
This law is ideal for solving triangles when two sides and the included angle (SAS) or all three sides (SSS) are known.
Formula: c² = a² + b² - 2ab*cos(C)
Special Triangle Cases
Isosceles Triangles
In an isosceles triangle, two sides are of equal length, and the angles opposite those sides are also equal. This property simplifies calculations when finding missing sides.
Equilateral Triangles
All sides and angles in an equilateral triangle are equal. The formula for the height of an equilateral triangle can also help in finding a missing side.
How Does Trigonometry Help in Triangle Calculations?
Trigonometry bridges the gap between angles and side lengths, making it easier to solve problems involving triangles of various types.
What Tools Can You Use to Solve Triangle Problems?
Mathematical tools like calculators, geometry software, and online platforms simplify the process of solving triangle-related problems.
Practical Applications of Triangle Calculations
From construction to navigation, knowing how to find the missing side of a triangle has countless real-world applications.
Common Mistakes to Avoid
Errors like misidentifying the hypotenuse or incorrectly applying formulas are common pitfalls. Double-check your work to avoid these mistakes.
Frequently Asked Questions
Q1: Can I use the Pythagorean theorem for all triangles?
No, it only applies to right triangles.
Q2: What if I only know the angles of a triangle?
You’ll need at least one side to calculate the others using trigonometry.
Q3: How do I find the height of a triangle?
Use the area formula or trigonometric ratios.
Q4: What’s the difference between sine and cosine?
Sine relates the opposite side to the hypotenuse, while cosine relates the adjacent side to the hypotenuse.
Q5: How accurate are online triangle calculators?
They’re generally accurate but double-check with manual calculations for critical problems.
Q6: Can triangles have sides of any length?
No, the side lengths must satisfy the triangle inequality rule.
Conclusion
Mastering how to find the missing side of a triangle opens the door to solving a wide variety of mathematical and practical problems. By understanding the properties of triangles and applying the appropriate formulas, you can tackle even the most challenging geometry questions with ease. Remember, practice makes perfect, so keep honing your skills!
- All About Tin Lizzy The Pioneering Rock Band That Shaped Music
- Ultimate Guide To Uc Davis Admissions Everything You Need To Know

how to find the missing side of a triangle Grace Evente1966
how to find the missing side of a triangle Grace Evente1966