Simple Ways To Turn Decimals Into Fractions And Master The Concept

Lawson Boehm 30 Jul 2025

Decimals and fractions: two different faces of the same mathematical coin. While decimals are great for precision, fractions often provide a clearer picture of proportions and relationships. But what if you need to switch between these two formats? Understanding how to turn decimals into fractions is not just a math exercise; it’s a skill that can simplify real-life problems, from cooking recipes to financial calculations.

Whether you're a student brushing up on your math skills, a professional dealing with data, or just someone curious about the concept, learning to convert decimals into fractions is easier than you think. With a solid grasp of the basic principles and a step-by-step approach, you can tackle this topic with confidence. Decimals and fractions may seem worlds apart, but they’re deeply interconnected in the language of mathematics.

In this comprehensive guide, we’ll break down the entire process into digestible steps, explore shortcuts, address common challenges, and answer frequently asked questions. By the end of this article, you’ll not only know how to turn decimals into fractions but also understand why it’s a useful skill to master. Let’s dive in!

What Are Decimals and Fractions?
Why Convert Decimals to Fractions?
How Do Decimals and Fractions Relate?
Step-by-Step Guide to Turn Decimals into Fractions
Terminating vs. Repeating Decimals
How to Handle Repeating Decimals in Fractions?
Simplifying Fractions Made Easy
Real-Life Applications of Decimals to Fractions
How Does Turning Decimals to Fractions Help in Math Problems?
Common Mistakes to Avoid
Tools and Calculators for Converting Decimals to Fractions
How to Turn Decimals into Fractions Manually?
Frequently Asked Questions
Conclusion

What Are Decimals and Fractions?

Decimals and fractions are two formats used to express parts of a whole. While decimals use a base-10 system to represent numbers, fractions divide a number into parts using a numerator (top) and a denominator (bottom). For instance, the decimal 0.5 is equivalent to the fraction 1/2. Understanding these formats lays the foundation for converting between them.

Why Convert Decimals to Fractions?

There are several scenarios where fractions are more practical than decimals. For example:

Fractions are often easier to visualize in geometric contexts, such as dividing a pie or a pizza.
In recipes, fractions provide more clarity when scaling ingredients.
Fractions can simplify algebraic operations and make solving equations more straightforward.

Converting decimals to fractions also enhances your mathematical versatility and allows you to approach problems from multiple perspectives.

How Do Decimals and Fractions Relate?

The relationship between decimals and fractions is straightforward: they are two ways of expressing the same value. A decimal can be written as a fraction by placing it over a power of 10. For example, 0.25 can be expressed as 25/100, which simplifies to 1/4. This relationship forms the basis for converting decimals to fractions.

Step-by-Step Guide to Turn Decimals into Fractions

Follow these steps to convert a decimal to a fraction:

Write the decimal as the numerator of a fraction.
Determine the place value of the decimal (e.g., tenths, hundredths) and set it as the denominator.
Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).

Example: Convert 0.75 to a fraction.

Step 1: Write 0.75 as 75/100.
Step 2: Simplify by dividing both numerator and denominator by 25. The result is 3/4.

Terminating vs. Repeating Decimals

Decimals can be classified into two types:

Terminating decimals: These have a finite number of digits, such as 0.5 or 0.125.
Repeating decimals: These have one or more digits that repeat indefinitely, such as 0.333... or 0.666...

The approach to converting each type into a fraction varies slightly, as we’ll explore below.

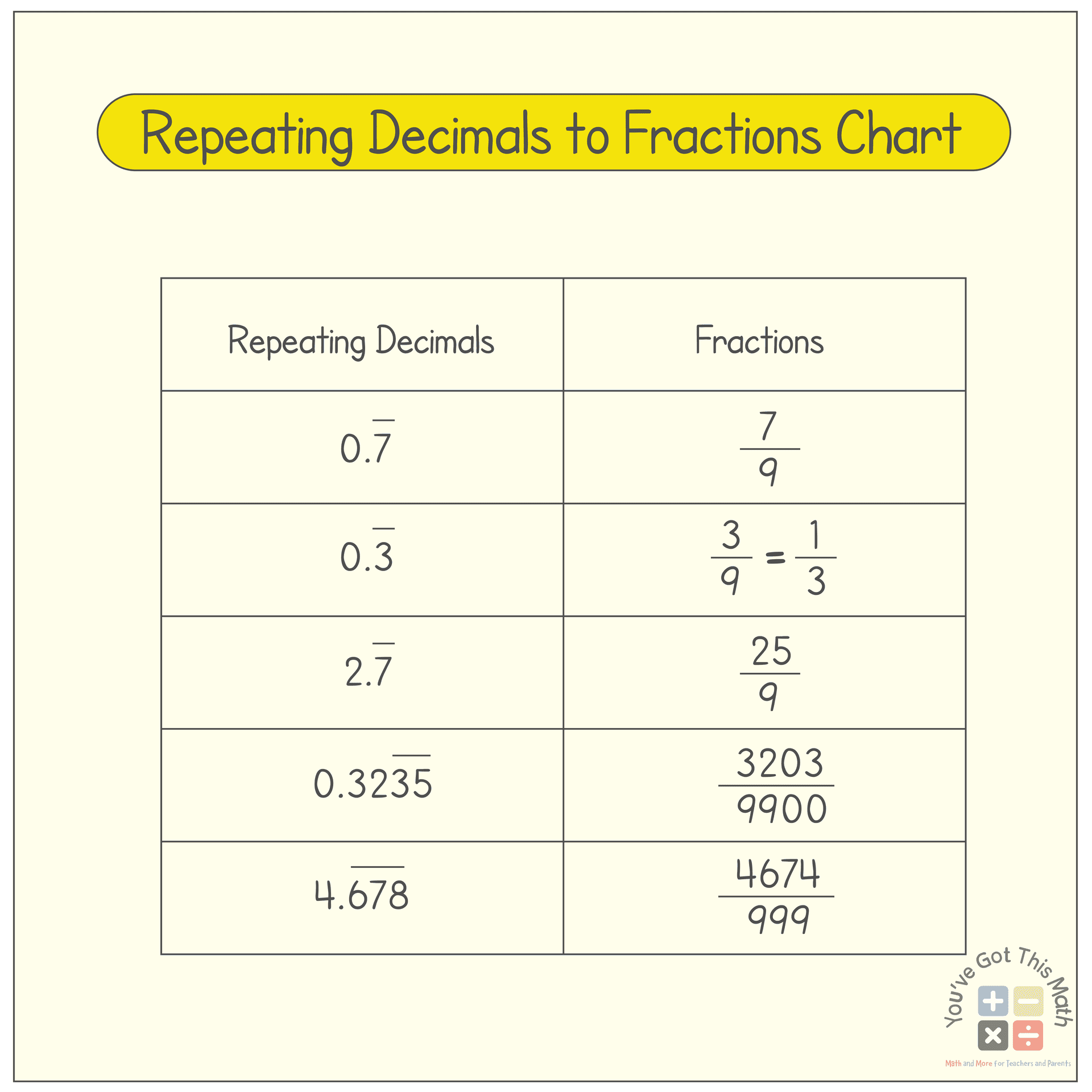
How to Handle Repeating Decimals in Fractions?

Converting repeating decimals to fractions involves a unique strategy:

Let x equal the repeating decimal (e.g., x = 0.333...).
Multiply x by a power of 10 that matches the length of the repeating sequence (e.g., 10x = 3.333...).
Subtract the original equation from this new equation to eliminate the repeating part (e.g., 10x - x = 3).
Solve for x to find the fraction (e.g., x = 3/9, which simplifies to 1/3).

Simplifying Fractions Made Easy

Simplifying fractions is a key step in the conversion process. To simplify:

Find the GCD of the numerator and denominator.
Divide both by the GCD to reduce the fraction to its simplest form.

For example, the fraction 50/100 simplifies to 1/2 by dividing both terms by 50.

Real-Life Applications of Decimals to Fractions

Decimals and fractions are used in various fields, including:

Finance: Calculating interest rates and discounts.
Engineering: Measuring dimensions and tolerances.
Science: Representing proportions and ratios.

The ability to convert between decimals and fractions enhances problem-solving skills across these and other domains.

How Does Turning Decimals to Fractions Help in Math Problems?

Fractions often simplify mathematical operations, such as addition, subtraction, and multiplication. For example:

Adding fractions with common denominators is more straightforward than adding decimals.
Fractions can reveal underlying patterns in sequences or functions.

By converting decimals to fractions, you can make complex problems more manageable.

Common Mistakes to Avoid

Here are some pitfalls to watch out for:

Failing to simplify the fraction fully.
Misidentifying the place value of the decimal.
Using incorrect arithmetic operations during conversion.

Practice and attention to detail can help you avoid these errors.

Tools and Calculators for Converting Decimals to Fractions

Several tools can assist in the conversion process:

Online calculators.
Mathematical software like MATLAB or Wolfram Alpha.
Apps designed for students and professionals.

While these tools are helpful, understanding the manual process is crucial for building mathematical intuition.

How to Turn Decimals into Fractions Manually?

To manually convert a decimal to a fraction:

Write the decimal as a fraction with a denominator of 1.
Multiply numerator and denominator by 10 until the decimal point is eliminated.
Simplify the resulting fraction.

Example: Convert 0.6 to a fraction.

Step 1: Write as 6/10.
Step 2: Simplify to 3/5.

Frequently Asked Questions

1. What is a repeating decimal?

A repeating decimal is a decimal with one or more digits that repeat indefinitely, such as 0.333...

2. Can all decimals be converted into fractions?

Yes, all decimals (both terminating and repeating) can be converted into fractions.

3. Do fractions always simplify to integers?

No, fractions represent parts of a whole and do not necessarily simplify to integers.

4. Are fractions better than decimals?

Neither is inherently better; the choice depends on context and the problem at hand.

5. How do you convert mixed decimals to fractions?

Separate the whole number and decimal parts, convert the decimal to a fraction, and combine them.

6. Is there a quick way to convert decimals to fractions?

For simple decimals, you can often identify the fraction by inspection, such as 0.5 = 1/2.

Conclusion

Mastering how to turn decimals into fractions is an essential skill that bridges the gap between two fundamental numerical formats. By following the steps outlined in this guide, you can confidently perform these conversions and apply them in various scenarios. Whether it’s for academic purposes, professional requirements, or everyday tasks, this knowledge empowers you to approach problems with clarity and precision.

Ready to convert decimals into fractions like a pro? Practice makes perfect, so grab a calculator, a notepad, and start solving!

$Converting decimals into fractions Study notes Latin Docsity$

Converting decimals into fractions Study notes Latin Docsity

15+ Free Converting Repeating Decimals to Fractions Worksheet Pages

CoreCurrent